njtynhj

当前條目的内容正在依照英語維基百科的内容进行翻译。（2019年1月28日） 如果您熟知條目内容并擅长翻译，欢迎协助改善或校对此條目，长期闲置的非中文内容可能会被移除。目前的翻译进度为： 50%

在光學中，色散是指一道光中，光的相速度隨著頻率而改變。^[1]擁有上述特性的介質，我們稱為色散性介質。提到色散，通常是指電磁波(包含可見光)的性質，但此性質可以推廣至任何波動，例如聲波與地震波的色散、波浪的色散、或是遠距傳遞時傳輸線模型或光纖的色散。

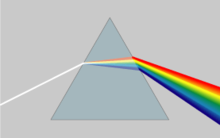
在一個色散的三稜鏡中，物質的色散效應使得不同顏色的光的折射角度不同，白光被分開。

在光學中，一個重要且常見的的色散現象為透過三稜鏡或是帶有色差的透鏡產生的光譜，不同顏色的光有著不同的折射角^[2]。在一些遠距傳輸的應用中，我們可以不考慮波的絕對相位，而只考慮波包的傳遞，在此情況下我們必須計算波包的色散，也就是頻率與不同群速度的波包的關係。

例子

彩虹可能是最常見的色散現象，其是由於色散造成白光在空間上分成不同波長(不同顏色)的部分。除此之外，色散亦發生在其他情況中，例如群速度色散造成波包在光纖中隨著傳輸距離而消散。

歷史

西元1666年，由牛頓所發現:太陽光(或日光燈等白色光)通過三棱鏡折射後，會被折射分散成紅、橙、黃、綠、藍、靛、紫等七種主要顏色的彩色光 → 稱為光的色散，分散的可見光帶稱為可見光譜。

自然光通過三棱镜后，因光的色散造成不同顏色（实质上是不同频率）的光折射到不同的方向，形成可见光谱

材料色散及波導色散

大部分情況下，色差色散指的是材料色散，也就是材料的的折射率隨著頻率而改變。在波導管中，有另一種色散稱為波導色散，其中產生色散的原因是因為幾何結構。廣義來說，"波導"色散可以發生於波經過任何不均勻的結構，而不論波是否侷限在特定空間中傳遞。在波導管裡，兩種色散會同時出現。在光纖中，此兩種色散剛好互相抵銷，因而可以傳遞特定波長的波，對於快速光纖通訊助益高。

光學中的材料色散

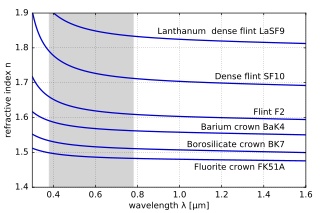
不同玻璃，真空折射率與波長的關係。可見光範圍以灰色區域表示。

在光學上，材料色散有優點也有缺點。透過三稜鏡，光的色散為製作光谱仪以及分光輻射計的基礎。有時候也會透過全像光柵，來達成更顯著的分光效果。然而，在透鏡中的色散效應造成影像品質低落，在顯微鏡、望遠鏡及其他成像技術上可見一斑。

在均勻介質中，波傳遞的相速度為

v=cndisplaystyle v=frac cn

c 為真空中的光速，而n為介質的折射率。

对于不同波长的光，介质的折射率n(λ)也不同。這個關係式通常由阿贝数可以計算出，或是由柯西等式或Sellmeier等式的係數求得。

由克拉莫-克若尼關係式，波長與實部折射率的關係與材料的吸收率有關，此吸收率由折射率的虛部(或稱消光係數)。在非磁性物質中，克拉莫-克若尼關係式的χ為電極化率χ_e = n² − 1.

对于可见光，一般的透明物质：

如果

λr>λy>λbdisplaystyle lambda _rm r>lambda _rm y>lambda _rm b

那麼

1<n(λr)<n(λy)<n(λb)displaystyle 1<n(lambda _rm r)<n(lambda _rm y)<n(lambda _rm b)

或可用以下表达式表示：

dndλ<0displaystyle frac dndlambda <0

在此狀況下，此介質擁有正常頻散。然而，當折射率隨著波長增加而增加時(通常在紫外光區發現^[4])，則介質被稱為擁有反常頻散。

法国数学家柯西发现折射率和光波长的关系，可以用一个级数表示：

n(λ)=B+Cλ2+Dλ4+⋯displaystyle n(lambda )=B+frac Clambda ^2+frac Dlambda ^4+cdots

其中B, C, D是三个柯西色散係数，由物质的种类决定。只需测定三个不同波长的光的折射率n(λ)，代入柯西色散公式中，便可得到三个联立方程式。解这组联立方程式就可以得到这种物质的三个柯西色散系数。有了三个柯西色散系数，就可以计算出其他波长的光的折射率，而不需要再进行测量。

除了柯西色散公式之外，还有其他的色散公式，如：Hartmann色散公式、Conrady色散公式、Hetzberger色散公式等。

群速度與相速度

在波導中的情況

寬頻中的高階色散

寶石學

顯影

中子星輻射

簡易的色散演示實驗（其一）

在日光下使用一桶水和一片鏡子就可以觀察光的色散現象了。为了便于观察现象，实验中光路需要較大的出射角来增大色散角度。此演示實驗中鏡子起到調整日光出射水面角度的作用。

参考文献

参见

• 光學頻譜