njtynhj

  本文介紹的是代数概念。關於几何定理，請見「圆幂定理」。

幂運算（英语：Exponentiation），又稱指數運算，是數學運算，表達式為bndisplaystyle b^n。其中，bdisplaystyle b稱為底數，而ndisplaystyle n稱為指數，通常指數寫成上標，放在底數的右邊。當不能用上標時，例如在編程語言或電子郵件中，bndisplaystyle b^n通常寫成b^n或b**n，也可視為超運算，記為b[3]n，亦可以用高德納箭號表示法，寫成b↑n，讀作“bdisplaystyle b的ndisplaystyle n次方”或「bdisplaystyle b的ydisplaystyle y次幂」。

若n為正整數, 可以把bndisplaystyle b^n看作乘方的结果, 等同於bdisplaystyle b自乘ndisplaystyle n次。

bn=b×⋯×b⏟ndisplaystyle b^n=underbrace btimes cdots times b _n

當指數為1時，通常不寫出來，因為運算出的值和底數的數值一樣；指數為2時，可以讀作“bdisplaystyle b的平方”；指數為 3 時，可以讀作“bdisplaystyle b的立方”。

起始值1（乘法的單位元）乘上底數（bdisplaystyle b）自乘指數（ndisplaystyle n）這麼多次。這樣定義了後，很易想到如何一般化指數 0 和負數的情況：除 0 外所有數的零次方都是 1 ；指數是負數時就等於重複除以底數（或底數的倒數自乘指數這麼多次），即：

b0=1displaystyle b^0=1qquad

b−n=1b×⋯×b⏟n=1bn=(1b)n(b≠0)displaystyle b^-n=1 over underbrace btimes cdots times b _n=frac 1b^n=left(frac 1bright)^nqquad (bneq 0)。

以分數為指數的冪定義為bmn=bmndisplaystyle b^frac mn=sqrt[n]b^m，即bdisplaystyle b的mdisplaystyle m次方再开ndisplaystyle n次方根

0的0次方（英语：zero to the power of zero）目前沒有數學家給予正式的定義。在部分數學領域中，如組合數學，常用的慣例是定義為 1 ，也有人主張定義為 1 。

因為在十进制，十的次方很易計算，只需在後面加零即可，所以科学记数法借此簡化記錄的數字；二的幂在計算機科學相當重要。

當n是複數及b是正實數時,

bn=exp⁡(nln⁡(b))displaystyle b^n=exp(nln(b))

exp是指數函數而 ln是自然對數。

重要的恆等式

运算法则

• 同底数幂相乘，底数不变，指数相加：

am×an=am+ndisplaystyle a^mtimes a^n=a^m+n

• 同底数幂相除，底数不变，指数相减：

am÷an=am−ndisplaystyle a^mdiv a^n=a^m-n

• 同指数幂相除，指数不变，底数相除：

anbn=(ab)ndisplaystyle frac a^nb^n=left(frac abright)^n

其他等式

• amn=amndisplaystyle a^frac mn=sqrt[n]a^m


• x−m=1xm(x≠0)displaystyle x^-m=frac 1x^mqquad (xneq 0)


• x0=1(x≠0)displaystyle x^0=1qquad (xneq 0)


• x1=xdisplaystyle x^1=x,!


• x−1=1x(x≠0)displaystyle x^-1=frac 1xqquad (xneq 0)


• xi=eiln⁡x=cos⁡(ln⁡x)+isin⁡(ln⁡x),i2=−1displaystyle x^i=e^iln x=cos(ln x)+isin(ln x),quad i^2=-1

运算律

加法和乘法存在交换律，比如：2+3=5=3+2displaystyle 2+3=5=3+2，2×3=6=3×2displaystyle 2times 3=6=3times 2，但是幂的运算不存在交换律，23=8displaystyle 2^3=8，但是32=9displaystyle 3^2=9。

同样，加法和乘法存在结合律，比如：(2+3)+4=9=2+(3+4)displaystyle (2+3)+4=9=2+(3+4)，(2×3)×4=24=2×(3×4)displaystyle (2times 3)times 4=24=2times (3times 4)，幂同样不存在：(23)4=84=4096displaystyle (2^3)^4=8^4=4096，但是2(34)=281=2,417,851,639,229,258,349,412,352displaystyle 2^(3^4)=2^81=2,417,851,639,229,258,349,412,352。

幂的运算顺序通常由上到下：

abc=a(bc)≠(ab)c=a(b×c)=ab×c.displaystyle a^b^c=a^(b^c)neq (a^b)^c=a^(btimes c)=a^btimes c.

整数指数幂

整数指数幂的运算只需要初等代数的知识。

正整数指数幂

表达式a2=a⋅adisplaystyle a^2=acdot a被称作adisplaystyle a的平方，因为边长为adisplaystyle a的正方形面积是a2displaystyle a^2。

表达式a3=a⋅a⋅adisplaystyle a^3=acdot acdot a被称作adisplaystyle a的立方，因为邊长为adisplaystyle a的正方体体积是a3displaystyle a^3。

所以32displaystyle 3^2读作3的平方，23displaystyle 2^3读作2的立方。

指数表示的是底数反复相乘多少次。比如35=3×3×3×3×3=243displaystyle 3^5=3times 3times 3times 3times 3=243，指数是5，底数是3，表示3反复相乘5次。

或者，整数指数幂可以递归地定义成：

an={1(n=0)a⋅an−1(n>0)(1a)−n(n<0)displaystyle a^n=begincases1&(n=0)\acdot a^n-1&(n>0)\left(frac 1aright)^-n&(n<0)endcases

指数是1或者0

注意31displaystyle 3^1表示仅仅1个3的乘积，就等于3。

注意35=3×34displaystyle 3^5=3times 3^4，34=3×33displaystyle 3^4=3times 3^3，33=3×32displaystyle 3^3=3times 3^2，32=3×31displaystyle 3^2=3times 3^1，

继续，得到31=3×30=3displaystyle 3^1=3times 3^0=3，所以30=1displaystyle 3^0=1

另一个得到此结论的方法是：通过运算法则xnxm=xn−mdisplaystyle frac x^nx^m=x^n-m

当m=ndisplaystyle m=n时，1=xnxn=xn−n=x0displaystyle 1=frac x^nx^n=x^n-n=x^0

• 任何数的1次方是它本身。

负数指数

我们定义任何不为0的数的-1次方等于它的倒数。

a−1=1a.displaystyle a^-1=frac 1a.

对于非零adisplaystyle a定义a−n=1andisplaystyle a^-n=frac 1a^n。因为当a=0displaystyle a=0时分母是0而没有意义。

这个定义是因为am⋅an=am+ndisplaystyle a^mcdot a^n=a^m+n，当m=−ndisplaystyle m=-n时

a−nan=a−n+n=a0=1,displaystyle a^-n,a^n=a^-n,+,n=a^0=1,

因为a0displaystyle a^0已经定义了，所以a−n=1andisplaystyle a^-n=frac 1a^n。

或者还可以像定义adisplaystyle a的0次方一样定义：

通过运算法则xmxn=xm−ndisplaystyle frac x^mx^n=x^m-n

当m=0displaystyle m=0时，可以约去分子得x−n=x0−n=x0xndisplaystyle x^-n=x^0-n=frac x^0x^n

负数指数a−ndisplaystyle a^-n还可以表示成1连续除以ndisplaystyle n个adisplaystyle a。比如：

3−4=13333=181=134displaystyle 3^-4=frac frac frac frac 13333=frac 181=frac 13^4.

特殊数的幂

10的幂

在十进制的计数系统中，10的幂写成1后面跟着很多个0。例如：103=1000, 10−3=0.001displaystyle 10^3=1000, 10^-3=0.001

因此10的幂用来表示非常大或者非常小的数字。如：299,792,458（真空中光速，单位是米每秒），可以写成 2.99792458×108displaystyle 2.99792458times 10^8，近似值 2.998×108displaystyle 2.998times 10^8.

国际单位制词头也使用10的幂来描述特别大或者特别小的数字，比如：词头“千”就是 103displaystyle 10^3，词头“毫”就是 10−3displaystyle 10^-3

2的幂

1的幂

1的任何次幂都为1

0的幂

0的正数幂都等于0。

0的负数幂没有定义。

任何非0之数的0次方都是1；而0的0次方是懸而未決的，某些領域下常用的慣例是約定為1。^[1]但某些教科書表示0的0次方為無意義。^[2]也有人主張定義為1。

负1的幂

-1的奇数幂等于-1

-1的偶数幂等于1

指数非常大时的幂

一个大于1的数的幂趋于无穷大，一个小于-1的数的幂趋于负无穷大

当a>1displaystyle a>1，n→∞displaystyle nto infty ，an→∞displaystyle a^nto infty

当a<−1displaystyle a<-1，n→∞displaystyle nto infty ，an→−∞displaystyle a^nto -infty

一个绝对值小于1的数的幂趋于0

当|a|<1displaystyle ，n→∞displaystyle nto infty ，an→0displaystyle a^nto 0

1的幂永远都是1

当a=1displaystyle a=1，n→∞displaystyle nto infty ，an→1displaystyle a^nto 1

如果数a趋于1而它的幂趋于无穷，那么极限并不一定是上面几个。一个很重要的例子是：

当n→∞,(1+1n)n→edisplaystyle nto infty ,left(1+frac 1nright)^nto e

参见e的幂

其他指数的极限参见幂的极限

正实数的实数幂

一个正实数的实数幂可以通过两种方法实现。

• 
  有理数幂可以通过N次方根定义，任何非0实数次幂都可以这样定义


• 
  自然对数可以被用来通过指数函数定义实数幂

N次方根

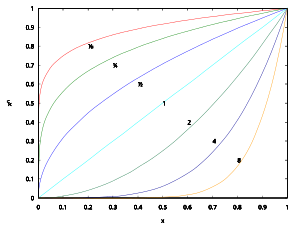
从上到下：x18, x14, x12, x1, x2, x4, x8displaystyle x^frac 18, x^frac 14, x^frac 12, x^1, x^2, x^4, x^8

一个数adisplaystyle a的ndisplaystyle n次方根是xdisplaystyle x，xdisplaystyle x使xn=adisplaystyle x^n=a。

如果adisplaystyle a是一个正实数，ndisplaystyle n是正整数，那么方程xn=adisplaystyle x^n=a只有一个正实数根。
这个根被称为adisplaystyle a的ndisplaystyle n次方根，记作：andisplaystyle sqrt[n]a，其中 displaystyle sqrt 叫做根号。或者，adisplaystyle a的ndisplaystyle n次方根也可以写成a1ndisplaystyle a^frac 1n.
例如412=2, 813=2displaystyle 4^frac 12=2, 8^frac 13=2

当指数是12displaystyle frac 12时根号上的2可以省略，如：4=42=2displaystyle sqrt 4=sqrt[2]4=2

有理数幂

有理数指数通常可以理解成

amn=(am)1n=amndisplaystyle a^frac mn=(a^m)^frac 1n=sqrt[n]a^m

e的幂

这个重要的数学常数e，有时叫做欧拉数，近似2.718，是自然对数的底。它提供了定义非整数指数幂的一个方法。
它是从以下极限定义的：

e=limn→∞(1+1n)ndisplaystyle e=lim _nto infty left(1+frac 1nright)^n

指数函数的定义是：

ex=limn→∞(1+xn)ndisplaystyle e^x=lim _nto infty left(1+frac xnright)^n

可以很简单地证明e的正整数k次方ekdisplaystyle e^k是：

ek=[limn→∞(1+1n)n]kdisplaystyle e^k=left[lim _nto infty left(1+frac 1nright)^nright]^k

=limn→∞[(1+1n)n]kdisplaystyle =lim _nto infty left[left(1+frac 1nright)^nright]^k

=limn→∞(1+kn⋅k)n⋅kdisplaystyle =lim _nto infty left(1+frac kncdot kright)^ncdot k

=limn⋅k→∞(1+kn⋅k)n⋅kdisplaystyle =lim _ncdot kto infty left(1+frac kncdot kright)^ncdot k

=limm→∞(1+km)mdisplaystyle =lim _mto infty left(1+frac kmright)^m

实数指数幂

y = b^x對各種底數b的圖像，分別為綠色的10、紅色的e、藍色的2和青色的1/2。

因为所有实数可以近似地表示为有理数，任意实数指数x可以定义成^[3]：

bx=limr→xbr,displaystyle b^x=lim _rto xb^r,

例如：

x≈1.732displaystyle xapprox 1.732

于是

5x≈51.732=5433250=5433250≈16.241displaystyle 5^xapprox 5^1.732=5^frac 433250=sqrt[250]5^433approx 16.241

实数指数幂通常使用对数来定义，而不是近似有理数。

自然对数ln⁡xdisplaystyle ln x是指数函数exdisplaystyle e^x的反函数。
它的定义是：对于任意b>0displaystyle b>0，满足

b=eln⁡bdisplaystyle b=e^ln b

根据对数和指数运算的规则：

bx=(eln⁡b)x=ex⋅ln⁡bdisplaystyle b^x=(e^ln b)^x=e^xcdot ln b

这就是实数指数幂的定义：

bx=ex⋅ln⁡bdisplaystyle b^x=e^xcdot ln b,

实数指数幂bxdisplaystyle b^x的这个定义和上面使用有理数指数和连续性的定义相吻合。对于复数，这种定义更加常用。

负实数的实数幂

如果adisplaystyle a是负数且ndisplaystyle n是偶数，那么xn=adisplaystyle x^n=a无实数解。
如果adisplaystyle a是负数且ndisplaystyle n是奇数，那么xn=adisplaystyle x^n=a有一个负数解。

使用对数和有理数指数都不能将akdisplaystyle a^k（其中adisplaystyle a是负实数，kdisplaystyle k实数）定义成实数。在一些特殊情况下，给出一个定义是可行的：负指数的整数指数幂是实数，有理数指数幂对于amndisplaystyle a^frac mn（ndisplaystyle n是奇数）可以使用ndisplaystyle n次方根来计算，但是因为没有实数xdisplaystyle x使x2=−1displaystyle x^2=-1，对于amndisplaystyle a^frac mn（ndisplaystyle n是偶数）时必须使用虚数单位idisplaystyle i。

使用对数的方法不能定义a≤0displaystyle aleq 0时的akdisplaystyle a^k为实数。实际上，exdisplaystyle e^x对于任何实数xdisplaystyle x都是正的，所以ln⁡(a)displaystyle ln(a)对于负数没有意义。

使用有理数指数幂来逼近的方法也不能用于负数adisplaystyle a因为它依赖于连续性。函数f(r)=ardisplaystyle f(r)=a^r对于任何正的有理数adisplaystyle a是连续的，但是对于负数adisplaystyle a，函数fdisplaystyle f在有些有理数rdisplaystyle r上甚至不是连续的。

例如：当a=−1displaystyle a=-1，它的奇数次根等于-1。所以如果ndisplaystyle n是正奇数整数，−1mn=−1displaystyle -1^frac mn=-1当mdisplaystyle m是奇数，−1mn=1displaystyle -1^frac mn=1当mdisplaystyle m是偶数。虽然有理数qdisplaystyle q使−1q=1displaystyle -1^q=1的集合是稠密集，但是有理数qdisplaystyle q使−1q=−1displaystyle -1^q=-1的集合也是。所以函数−1qdisplaystyle -1^q在有理数域不是连续的。

正实数的复数幂

e的虚数次幂

指数函数e^z可以通过(1 + z/N)^N当N趋于无穷大时的极限来定义，那么e^iπ就是(1 + iπ/N)^N的极限。在这个动画中n从1取到100。(1 + iπ/N)^N的值通过N重复增加在复数平面上展示，最终结果就是(1 + iπ/N)^N的准确值。可以看出，随着N的增大，(1 + iπ/N)^N逐渐逼近极限-1。这就是欧拉公式。

复数运算的几何意义和e的幂可以帮助我们理解eixdisplaystyle e^ix（xdisplaystyle x是实数）。想象一个直角三角形(0,1,1+ixn)displaystyle (0,1,1+frac ixn)（括号内是复数平面内三角形的三个顶点），对于足够大的ndisplaystyle n，这个三角形可以看作一个扇形，这个扇形的中心角就等于xndisplaystyle frac xn弧度。对于所有kdisplaystyle k，三角形(0,(1+ixn)k,(1+ixn)k+1)displaystyle (0,(1+frac ixn)^k,(1+frac ixn)^k+1)互为相似三角形。所以当ndisplaystyle n足够大时(1+ixn)ndisplaystyle (1+frac ixn)^n的极限是复数平面上的单位圆上xdisplaystyle x弧度的点。这个点的极坐标是(r,θ)=(1,x)displaystyle (r,theta )=(1,x)，直角坐标是(cos⁡x,sin⁡x)displaystyle (cos x,sin x)。所以eix=cos⁡x+isin⁡xdisplaystyle e^ix=cos x+isin x。这就是欧拉公式，它通过复数的意义将代数学和三角学联系起来了。

等式ez=1displaystyle e^z=1的解是一个整数乘以2iπdisplaystyle 2ipi ^[4]：

z:ez=1=2kπi:k∈Z.displaystyle z:e^z=1=2kpi i:kin mathbb Z .

更一般地，如果eb=adisplaystyle e^b=a，那么ez=adisplaystyle e^z=a的每一个解都可以通过将2iπdisplaystyle 2ipi 的整数倍加上bdisplaystyle b得到：

z:ez=a=b+2kπi:k∈Z.displaystyle z:e^z=a=b+2kpi i:kin mathbb Z .

这个复指数函数是一个有周期2iπdisplaystyle 2ipi 的周期函数。

更简单的：eiπ=−1; ex+iy=ex(cos⁡y+isin⁡y)displaystyle e^ipi =-1; e^x+iy=e^x(cos y+isin y)。

三角函数

根据欧拉公式，三角函数余弦和正弦是：

cos⁡z=ei⋅z+e−i⋅z2sin⁡z=ei⋅z−e−i⋅z2⋅idisplaystyle cos z=frac e^icdot z+e^-icdot z2qquad sin z=frac e^icdot z-e^-icdot z2cdot i

历史上，在复数发明之前，余弦和正弦是用几何的方法定义的。上面的公式将复杂的三角函数的求和公式转换成了简单的指数方程

ei⋅(x+y)=ei⋅x⋅ei⋅y.displaystyle e^icdot (x+y)=e^icdot xcdot e^icdot y.,

使用了复数指数幂之后，很多三角学问题都能够使用代数方法解决。

e的复数指数幂

ex+iydisplaystyle e^x+iy可以分解成ex⋅eiydisplaystyle e^xcdot e^iy。其中exdisplaystyle e^x是ex+iydisplaystyle e^x+iy的模，eiydisplaystyle e^iy决定了ex+iydisplaystyle e^x+iy的方向

正实数的复数幂

如果adisplaystyle a是一个正实数，zdisplaystyle z是任何复数，azdisplaystyle a^z定义成ez⋅ln⁡(a)displaystyle e^zcdot ln(a)，其中x=ln⁡(a)displaystyle x=ln(a)是方程ex=adisplaystyle e^x=a的唯一解。所以处理实数的方法同样可以用来处理复数。

例如：

2i=ei⋅ln⁡(2)=cos⁡ln⁡2+i⋅sin⁡ln⁡2=0.7692+0.63896idisplaystyle 2^i=e^icdot ln(2)=cos ln 2+icdot sin ln 2=0.7692+0.63896i

ei=0.54030+0.84147idisplaystyle e^i=0.54030+0.84147i

10i=−0.66820+0.74398idisplaystyle 10^i=-0.66820+0.74398i

(e2π)i=535.49i=1displaystyle (e^2pi )^i=535.49^i=1

在函數中

當函數名後有上標的數（即函數的指數），一般指要重複它的運算。例如f3(x)displaystyle f^3(x)即f(f(f(x)))displaystyle f(f(f(x)))。特別地，f−1(x)displaystyle f^-1(x)指f(x)displaystyle f(x)的反函數。

但三角函数的情況有所不同，一個正指數應用於函數的名字時，指答案要進行乘方運算，而指數為-1時则表示其反函數。例如：(sin⁡x)−1displaystyle (sin x)^-1表示csc⁡xdisplaystyle csc x。因此在三角函數時，使用sin−1⁡xdisplaystyle sin ^-1x來表示sin⁡xdisplaystyle sin x的反函數arcsin⁡xdisplaystyle arcsin x。

在抽象代數中

计算自然数（正整数）ndisplaystyle n的andisplaystyle a^n的算法

最快的方式计算andisplaystyle a^n，当ndisplaystyle n是正整数的时候。它利用了测试一个数是奇数在计算机上是非常容易的，和通过简单的移所有位向右来除以2的事实。

偽代碼：

 1. 1 → y, n → k, a → f
 2.若k不為0,執行3至6
 3.若k為奇數, y * f → y
 4. k [[位操作#移位|右移]]1位（即k / 2 → k ,小數點無條件捨去）
 5. f * f → f
 6.回到2
 7.傳回y

在C/C++语言中，你可以写如下算法：

 double power (double a, unsigned int n)
 
 double y = 1;
 double f = a;
 unsigned int k = n;
 while (k != 0) 
 if (k % 2 == 1) y *= f;
 k >>= 1;
 f *= f;
 
 return y;
 

此算法的時間複雜度為O(log⁡n)displaystyle mathrm O (log n)!，比普通算法快（a自乘100次，時間複雜度為O(n)displaystyle mathrm O (n)!），在ndisplaystyle n較大的時候更為顯著。

例如計算a100displaystyle a^100，普通算法需要算100次，上述算法則只需要算7次。若要計算an(n<0)displaystyle a^n(n<0)可先以上述算法計算a|n|displaystyle a^n，再作倒數。

註釋

另見

• 迭代冪次

外部連結

• 指數的歷史