njtynhj

線性函數（紅色）會作用估算函數f(x)displaystyle f(x) （藍色）。

梯形公式是數學中数值积分的基础公式之一：∫abf(x)dx≈(b−a)f(a)+f(b)2.displaystyle int _a^bf(x),dxapprox (b-a)frac f(a)+f(b)2.

公式由来

由积分中值定理可得

∃ξ∈[a,b]∫abf(x)dx=(b−a)f(ξ)displaystyle exists xi in [a,b]int limits _a^bf(x)dx=(b-a)f(xi )，

但由于ξ其值一般难于确定，故难以准确算出f(ξ)的值。

如果用两端点f(a)与f(b)的算术平均值估算f(ξ)，有

∫abf(x)dx≈b−a2[f(a)+f(b)]displaystyle int limits _a^bf(x)dxapprox frac b-a2[f(a)+f(b)]，

这就是梯形公式。

类似地，如果用区间中点c=a+b2displaystyle c=frac a+b2其高度f(c)取代f(ξ)，从而有中矩形公式

∫abf(x)dx≈(b−a)f(a+b2)displaystyle int limits _a^bf(x)dxapprox (b-a)f(frac a+b2)。

复合求积公式

每一區間相同

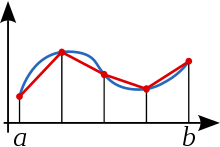
梯形公式的示意圖（長度相同的區間）。

為了計算出更加準確的定積分，可以把積分的區間[a,b]displaystyle [a,b]分成Ndisplaystyle N份，當中Ndisplaystyle N趨向無限，分割出的每一個區間長度必定要是一樣的，然後就可以應用梯形公式：

∫abf(x)dx≈b−aN[f(a)+f(b)2+∑k=1N−1f(a+kb−aN)].displaystyle int _a^bf(x),dxapprox frac b-aNleft[f(a)+f(b) over 2+sum _k=1^N-1fleft(a+kfrac b-aNright)right].

亦可以寫成：

∫abf(x)dx≈b−a2N(f(x0)+2f(x1)+2f(x2)+⋯+2f(xN−1)+f(xN))displaystyle int _a^bf(x),dxapprox frac b-a2Nleft(f(x_0)+2f(x_1)+2f(x_2)+cdots +2f(x_N-1)+f(x_N)right)

當中

xk=a+kb−aN, for k=0,1,…,Ndisplaystyle x_k=a+kfrac b-aN,text for k=0,1,dots ,N

其余项为

Rn(f)=−b−a12h2f″(η),η∈(a,b)displaystyle R_n(f)=-frac b-a12h^2f''(eta ),eta in (a,b)

當區間的長度並不相同時，這一條公式便不能使用。

每一區間並不相同

梯形公式的示意圖（長度不相同的區間）

給予x1,…,xNdisplaystyle x_1,ldots ,x_N以及y1,…,yNdisplaystyle y_1,ldots ,y_N，定積分就可以估算成

∫abf(x)dx≈12∑i=2N(xi−xi−1)(yi+yi−1)displaystyle int _a^bf(x),dxapprox frac 12sum _i=2^N(x_i-x_i-1)(y_i+y_i-1),

當中

yi=f(xi)displaystyle y_i=f(x_i).

誤差分析

應用梯形公式的誤差值是真值數字與運用梯形公式結果的差異：

error=∫abf(x)dx−b−aN[f(a)+f(b)2+∑k=1N−1f(a+kb−aN)]displaystyle texterror=int _a^bf(x),dx-frac b-aNleft[f(a)+f(b) over 2+sum _k=1^N-1fleft(a+kfrac b-aNright)right]

如果 (a, b) 中存在一個實數ξ，那麼

error=−(b−a)312N2f″(ξ)displaystyle texterror=-frac (b-a)^312N^2f''(xi )

对于中矩形公式，其误差类似的有：

error=−(b−a)324f″(ξ)displaystyle texterror=-frac (b-a)^324f''(xi )

如果被積函數是一個凸函數（亦即有一個正值二階導數），那麼誤差會是一個負數，也代表梯形公式的估算值高估了真實數字。這可以利用一個幾何圖形代去表達：梯形不但覆蓋曲線下的面積更超越其範圍。同樣地，如果被積函數是一個凹函數，梯形公式就會低估其真實數字因為曲線下部份面積沒有被計算在內。如果被積函數中有拐點。它的錯誤是比較難去估計。

一般而言有數種方法可以去分析誤差，例如是：傅利葉級數。

在N → ∞的情況下，趨向性的估計誤差是：

error=−(b−a)212N2[f′(b)−f′(a)]+O(N−3).displaystyle texterror=-frac (b-a)^212N^2big [f'(b)-f'(a)big ]+O(N^-3).

参考文献

• 《数值分析》，清华大学出版社，李庆扬等编，书号ISBN 978-7-302-18565-9