njtynhj

在积分学中，椭圆积分最初出现于椭圆的弧长有关的问题中。Guilio Fagnano和欧拉是最早的研究者。现代数学将椭圆积分定义为可以表达为如下形式的任何函数 fdisplaystyle f,的积分

f(x)=∫cxR[t,P(t)] dtdisplaystyle f(x)=int _c^xR[t,sqrt[]P(t)] dt,!

其中Rdisplaystyle R,是其两个参数的有理函数，Pdisplaystyle P,是一个无重根的3displaystyle 3,或4displaystyle 4,阶多项式，而cdisplaystyle c,是一个常数。

通常，椭圆积分不能用基本函数表达。这个一般规则的例外出现在Pdisplaystyle P,有重根的时候，或者是Rdisplaystyle R,,(x,y)displaystyle left(x,yright),没有ydisplaystyle y,的奇数幂时。但是，通过适当的简化公式，每个椭圆积分可以变为只涉及有理函数和三个经典形式的积分。（也即，第一，第二，和第三类的椭圆积分）。

除下面给出的形式之外，椭圆积分也可以表达为勒让德形式和Carlson对称形式。通过对施瓦茨-克里斯托费尔映射的研究可以加深对椭圆积分理论的理解。历史上，椭圆函数是作为椭圆积分的逆函数被发现的，特别是这一个：F[sn(z;k);k]=zdisplaystyle F[textrm snleft(z;kright);k]=z,其中sndisplaystyle textrm sn,是雅可比椭圆函数之一。

记法

椭圆积分通常表述为不同变量的函数。这些变量完全等价（它们给出同样的椭圆积分），但是它们看起来很不相同。很多文献使用单一一种标准命名规则。在定义积分之前，先来检视一下这些变量的命名常规：

• 
  αdisplaystyle alpha 模角;


• 
  k=sin⁡αdisplaystyle k=sin alpha 椭圆模;


• 
  m=k2=sin2⁡αdisplaystyle m=k^2=sin ^2alpha 参数;

上述三种常规完全互相确定。规定其中一个和规定另外一个一样。椭圆积分也依赖于另一个变量，可以有如下几种不同的设定方法：

• 
  ϕdisplaystyle phi ,! 幅度
  


• 
  xdisplaystyle x, 其中x=sin⁡ϕ=snudisplaystyle x=sin phi =textrm sn;u,!
  


• 
  udisplaystyle u,，其中x=snudisplaystyle x=textrm sn;u,而sndisplaystyle textrm sn,是雅可比椭圆函数之一

规定其中一个决定另外两个。这样，它们可以互换地使用。注意udisplaystyle u,也依赖于mdisplaystyle m,。其它包含udisplaystyle u,的关系有

cos⁡ϕ=cnudisplaystyle cos phi =textrm cn;u,!

和

1−msin2⁡ϕ=dnu.displaystyle sqrt 1-msin ^2phi =textrm dn;u.,!

后者有时称为δ幅度并写作Δ(ϕ)=dnudisplaystyle Delta (phi )=textrm dn;u,!。有时文献也称之为补参数，补模或者补模角。这些在四分周期中有进一步的定义。

第一类不完全椭圆积分

第一类不完全椭圆积分 Fdisplaystyle F,定义为

F(ϕ∖α)=F(ϕ|m)=∫0ϕdθ1−(sin⁡θsin⁡α)2.m)=int _0^phi frac rm dtheta sqrt 1-(sin theta sin alpha )^2.,!

与此等价，用雅可比的形式，可以设
x=sin⁡ϕ , t=sin⁡θdisplaystyle x=sin phi ~,~t=sin theta ;!；则

F(ϕ∖α)=F(x;k)=∫0xdt(1−t2)(1−k2t2)displaystyle F(phi setminus alpha )=F(x;k)=int _0^xfrac rm dtsqrt (1-t^2)(1-k^2t^2),!

其中，假定任何有竖直条出现的地方，紧跟竖直条的变量是（如上定义的）参数；而且，当反斜杠出现的时候，跟着出现的是模角。
在这个意义下，F(sin⁡ϕ;sin⁡α)=F(ϕ|sin2⁡α)=F(ϕ∖α) sin ^2alpha )=F(phi setminus alpha )~,!，这里的记法来自标准参考书Abramowitz and Stegun。

但是，还有许多不同的用于椭圆积分的记法。取值为椭圆积分的函数没有（象平方根，正弦和误差函数那样的）标准和唯一的名字。甚至关于该领域的文献也常常采用不同的记法。Gradstein, Ryzhik[1], Eqdisplaystyle Eq,.(8.111)]采用F(ϕ,k)displaystyle F(phi ,k),!。该记法和这里的F(ϕ|k2) displaystyle F(phi ；以及下面的E(ϕ,k)=E(ϕ|k2) displaystyle E(phi ,k)=E(phi 等价。

和上面的不同对应的是，如果从Mathematica语言翻译代码到Maple语言，必须将EllipticK函数的参数用它的平方根代替。反过来，如果从Maple翻到Mathematica，则参数应该用它的平方代替。Maple中的EllipticK(xdisplaystyle x)几乎和Mathematica中的EllipticK[x2displaystyle x^2]相等；至少当0<x<1displaystyle 0<x<1,时是相等的。

注意

F(x;k)=udisplaystyle F(x;k)=u,!

其中udisplaystyle u,如上文所定义：由此可见，雅可比椭圆函数是椭圆积分的逆。

加法公式

F(x1;k)+F(x2;k)=F(arcsin⁡cos⁡x21−k2sin2⁡x2sin⁡x1+cos⁡x11−k2sin2⁡x1sin⁡x21−k2sin2⁡x1sin2⁡x2;k)displaystyle F(x_1;k)+F(x_2;k)=Fleft(arcsin frac cos x_2sqrt 1-k^2sin ^2x_2sin x_1+cos x_1sqrt 1-k^2sin ^2x_1sin x_21-k^2sin ^2x_1sin ^2x_2;kright),!

性质

F(x+nπ;k)=F(x;k)+2nK(k)displaystyle F(x+npi ;k)=F(x;k)+2nK(k),!

F(x+nπ2;k)=nK(k)displaystyle F(x+frac npi 2;k)=nK(k),!

n∈Zdisplaystyle nin mathbb Z ,!

F(−x;k)=−F(x;k)displaystyle F(-x;k)=-F(x;k),!

F(x;0)=0displaystyle F(x;0)=0,!

F(0;k)=−F(x;k)displaystyle F(0;k)=-F(x;k),!

F(x;1)=arctanhsin⁡xdisplaystyle F(x;1)=rm arctanhsin x,!

−π2<ℜ(x)<π2displaystyle -frac pi 2<Re (x)<frac pi 2,!

第一类不完全椭圆积分的导数

ddxF(x;k)=11−k2sin2⁡xdisplaystyle frac rm drm dxF(x;k)=frac 1sqrt 1-k^2sin ^2x,!

ddkF(x;k)=E(x;k)2k(1−k)−F(x;k)2k−sin⁡2x4(1−k)1−ksin2⁡xdisplaystyle frac rm drm dkF(x;k)=frac E(x;k)2k(1-k)-frac F(x;k)2k-frac sin 2x4(1-k)sqrt 1-ksin ^2x,!

第二类不完全椭圆积分

第二类不完全椭圆积分 Edisplaystyle E!是

E(ϕ∖α)=E(ϕ|m)=∫0ϕE′(θ) dθ=∫0ϕ1−(sin⁡θsin⁡α)2 dθ.displaystyle E(phi setminus alpha )=E(phi

与此等价，采用另外一个记法（作变量替换t=sin⁡θdisplaystyle t=sin theta ,!），

E(x;k)=∫0x1−k2t21−t2 dt.displaystyle E(x;k)=int _0^xfrac sqrt 1-k^2t^2sqrt 1-t^2 rm dt.,!

其它关系包括

E(ϕ|m)=∫0udn2wdw=u−m∫0usn2wdw=(1−m)u+m∫0ucn2wdw.m)=int _0^utextrm dn^2w;rm dw=u-mint _0^utextrm sn^2w;rm dw=(1-m)u+mint _0^utextrm cn^2w;rm dw.,!

E(ϕ|k2)=(1−k2)∫0ϕdθ(1−k2sin2⁡θ)1−k2sin2⁡θ+k2sin⁡θcos⁡θ1−k2sin2⁡θdisplaystyle E(phi

加法公式

E(x1;k)+E(x2;k)=E(arcsin⁡cos⁡x21−k2sin2⁡x2sin⁡x1+cos⁡x11−k2sin2⁡x1sin⁡x21−k2sin2⁡x1sin2⁡x2;k)displaystyle E(x_1;k)+E(x_2;k)=Eleft(arcsin frac cos x_2sqrt 1-k^2sin ^2x_2sin x_1+cos x_1sqrt 1-k^2sin ^2x_1sin x_21-k^2sin ^2x_1sin ^2x_2;kright),!

+k2sin2⁡x1sin⁡x2cos⁡x21−k2sin2⁡x2+k2sin⁡x1sin2⁡x2cos⁡x11−k2sin2⁡x11−k2sin2⁡x1sin2⁡x2displaystyle +frac k^2sin ^2x_1sin x_2cos x_2sqrt 1-k^2sin ^2x_2+k^2sin x_1sin ^2x_2cos x_1sqrt 1-k^2sin ^2x_11-k^2sin ^2x_1sin ^2x_2,!

性质

E(ϕ+nπ;k)=E(ϕ;k)+2nE(k)displaystyle E(phi +npi ;k)=E(phi ;k)+2nE(k),!

E(−ϕ;k)=−E(ϕ;k)displaystyle E(-phi ;k)=-E(phi ;k),!

第二类不完全椭圆积分的导数

ddϕE(ϕ;k)=1−k2sin2⁡ϕdisplaystyle frac rm drm dphi E(phi ;k)=sqrt 1-k^2sin ^2phi ,!

ddkE(ϕ;k)=E(ϕ;k)−F(ϕ;k)2kdisplaystyle frac rm drm dkE(phi ;k)=frac E(phi ;k)-F(phi ;k)2k,!

dndknE(ϕ;k)=π2kn2F1(−12,12;1−n;k)−πcos⁡ϕ2k2nF2×1×01×3×2[12;−12,12,1;12,1;1,32;1−n;;−k2cos⁡ϕ,cos2⁡ϕ]+πm1−ncos⁡ϕ8F3×1×12×1×1[12,32,2;12,1;2,2−n;1−n;32;32;−k2cos2⁡ϕ,k2]displaystyle frac rm d^nrm dk^nE(phi ;k)=frac pi 2k^n_2F_1left(-frac 12,frac 12;1-n;kright)-frac sqrt pi cos phi 2k^2nF_2times 1times 0^1times 3times 2beginbmatrixfrac 12;-frac 12,frac 12,1;frac 12,1;\1,frac 32;1-n;;\-k^2cos phi ,cos ^2phi endbmatrix+frac pi m^1-ncos phi 8F_3times 1times 1^2times 1times 1beginbmatrixfrac 12,frac 32,2;frac 12,1;\2,2-n;1-n;frac 32;frac 32;\-k^2cos ^2phi ,k^2endbmatrix,!

第三类不完全椭圆积分

第三类不完全椭圆积分Πdisplaystyle Pi ,!是

Π(n;ϕ|m)=∫0ϕdθ(1−nsin2⁡θ)1−(sin⁡θsin⁡oε)2,m)=int _0^phi frac rm dtheta (1-nsin ^2theta )sqrt 1-(sin theta sin o!varepsilon )^2,,!

或者

Π(n;ϕ|m)=∫0sin⁡ϕdt(1−nt2)(1−k2t2)(1−t2),m)=int _0^sin phi frac rm dt(1-nt^2)sqrt (1-k^2t^2)(1-t^2),,!

或者

Π(n;ϕ|m)=∫0F(ϕ|m)dw1−nsn2(w|m).m)=int _0^F(phi frac rm dw1-ntextrm sn^2(w.;,!

数字ndisplaystyle n,称为特征数，可以取任意值，和其它参数独立。但是要注意Π(1;π2|m)displaystyle Pi (1;frac pi 2对于任意mdisplaystyle m,!是无穷的。

加法公式

Π(n;ϕ1,k)+Π(n;ϕ2,k)=Π[n;arccos⁡cos⁡ϕ1cos⁡ϕ2−sin⁡ϕ1sin⁡ϕ2(1−k2sin2⁡ϕ1)(1−k2sin2⁡ϕ2)1−k2sin2⁡ϕ1sin⁡ϕ2,k]−n(1−n)(n−k2)arctan⁡(1−n)n(n−k2)sin⁡arccos⁡cos⁡ϕ1cos⁡ϕ2−sin⁡ϕ1sin⁡ϕ2(1−k2sin2⁡ϕ1)(1−k2sin2⁡ϕ2)1−k2sin2⁡ϕ1sin⁡ϕ2sin⁡ϕ1sin⁡ϕ2ncos⁡ϕ1cos⁡ϕ2−nsin⁡ϕ1sin⁡ϕ2(1−k2sin2⁡ϕ1)(1−k2sin2⁡ϕ2)1−k2sin2⁡ϕ1sin⁡ϕ21−k2sin2⁡arccos⁡cos⁡ϕ1cos⁡ϕ2−sin⁡ϕ1sin⁡ϕ2(1−k2sin2⁡ϕ1)(1−k2sin2⁡ϕ2)1−k2sin2⁡ϕ1sin⁡ϕ2sin⁡ϕ1sin⁡ϕ2+1−nsin2⁡arccos⁡cos⁡ϕ1cos⁡ϕ2−sin⁡ϕ1sin⁡ϕ2(1−k2sin2⁡ϕ1)(1−k2sin2⁡ϕ2)1−k2sin2⁡ϕ1sin⁡ϕ2displaystyle Pi (n;phi _1,k)+Pi (n;phi _2,k)=Pi left[n;arccos frac cos phi _1cos phi _2-sin phi _1sin phi _2sqrt (1-k^2sin ^2phi _1)(1-k^2sin ^2phi _2)1-k^2sin ^2phi _1sin phi _2,kright]-sqrt frac n(1-n)(n-k^2)arctan frac sqrt (1-n)n(n-k^2)sin arccos frac cos phi _1cos phi _2-sin phi _1sin phi _2sqrt (1-k^2sin ^2phi _1)(1-k^2sin ^2phi _2)1-k^2sin ^2phi _1sin phi _2sin phi _1sin phi _2frac ncos phi _1cos phi _2-nsin phi _1sin phi _2sqrt (1-k^2sin ^2phi _1)(1-k^2sin ^2phi _2)1-k^2sin ^2phi _1sin phi _2sqrt 1-k^2sin ^2arccos frac cos phi _1cos phi _2-sin phi _1sin phi _2sqrt (1-k^2sin ^2phi _1)(1-k^2sin ^2phi _2)1-k^2sin ^2phi _1sin phi _2sin phi _1sin phi _2+1-nsin ^2arccos frac cos phi _1cos phi _2-sin phi _1sin phi _2sqrt (1-k^2sin ^2phi _1)(1-k^2sin ^2phi _2)1-k^2sin ^2phi _1sin phi _2

第三类不完全椭圆积分的导数

∂∂nΠ(n;ϕ,k)=12(k2−n)(n−1)[E(ϕ;k)+(k2−n)F(ϕ;k)n+(n2−k2)Π(n;ϕ,k)n−n1−k2sin⁡ϕsin⁡2ϕ2(1−nsin2⁡ϕ)]displaystyle frac partial partial nPi (n;phi ,k)=frac 12(k^2-n)(n-1)left[E(phi ;k)+frac (k^2-n)F(phi ;k)n+frac (n^2-k^2)Pi (n;phi ,k)n-frac nsqrt 1-k^2sin phi sin 2phi 2(1-nsin ^2phi )right]

∂m∂nmΠ(n;ϕ,k)=sin⁡ϕnm∑q=0∞q!(nsin2⁡ϕ)q(2q+1)Γ(q−m+1)F1(q+12,12,12;q+32;sin2⁡ϕ,k2sin2⁡ϕ)displaystyle frac partial ^mpartial n^mPi (n;phi ,k)=frac sin phi n^msum _q=0^infty frac q!(nsin ^2phi )^q(2q+1)Gamma (q-m+1)F_1left(q+frac 12,frac 12,frac 12;q+frac 32;sin ^2phi ,k^2sin ^2phi right)

∂∂ϕΠ(n;ϕ,k)=1(1−k2sin2⁡ϕ)displaystyle frac partial partial phi Pi (n;phi ,k)=frac 1(1-k^2sin ^2phi )!

∂∂kΠ(n;ϕ,k)=kn−k2[E(ϕ;k)k2−1+Π(n;ϕ,k)−k2sin⁡2ϕ2(k2−1)1−k2sin2⁡ϕ]displaystyle frac partial partial kPi (n;phi ,k)=frac kn-k^2left[frac E(phi ;k)k^2-1+Pi (n;phi ,k)-frac k^2sin 2phi 2(k^2-1)sqrt 1-k^2sin ^2phi right]!

特殊值

Π(n;ϕ,1)=12n−2[nln⁡1+nsin⁡ϕ1−nsin⁡ϕ−2ln⁡(sec⁡ϕ+tan⁡ϕ)]displaystyle Pi (n;phi ,1)=frac 12n-2left[sqrt nln frac 1+sqrt nsin phi 1-sqrt nsin phi -2ln(sec phi +tan phi )right]!

−π2≤ℜ(ϕ)≤π2displaystyle -frac pi 2leq Re (phi )leq frac pi 2!

Π(0;ϕ,k)=F(ϕ,k)displaystyle Pi (0;phi ,k)=F(phi ,k)!

Π(n;ϕ,0)=arctanh(n−1tan⁡ϕ)n−1displaystyle Pi (n;phi ,0)=frac rm arctanh(sqrt n-1tan phi )sqrt n-1!

−π2≤ℜ(ϕ)≤π2displaystyle -frac pi 2leq Re (phi )leq frac pi 2!

Π(n;ϕ,n)=11−n[E(ϕ,n)−nsin⁡2ϕ21−nsin2⁡ϕ]displaystyle Pi (n;phi ,sqrt n)=frac 11-nleft[E(phi ,sqrt n)-frac nsin 2phi 2sqrt 1-nsin ^2phi right]!

Π(n;1k,k)=1kΠ(nk2,1k)displaystyle Pi left(n;frac 1k,kright)=frac 1kPi left(frac nk^2,frac 1kright)!

Π(1;ϕ,k)=1−k2sin2⁡ϕtan⁡ϕ−E(ϕ,k)1−k2+F(ϕ,k)displaystyle Pi left(1;phi ,kright)=frac sqrt 1-k^2sin ^2phi tan phi -E(phi ,k)1-k^2+F(phi ,k)!

第一类完全椭圆积分

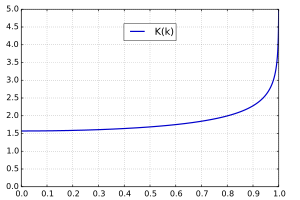
第一类完全椭圆积分K(k)displaystyle K(k)

如果幅度为π2displaystyle frac pi 2,或者x=1displaystyle x=1,，则称椭圆积分为完全的。
第一类完全椭圆积分Kdisplaystyle K,可以定義为

K(k)=∫0π2dθ1−k2sin2⁡θdisplaystyle K(k)=int _0^frac pi 2frac rm dtheta sqrt 1-k^2sin ^2theta

或者

K(k)=∫01dt(1−t2)(1−k2t2).displaystyle K(k)=int _0^1frac rm dtsqrt (1-t^2)(1-k^2t^2).!

它是第一类不完全椭圆积分的特例：

K(k)=F(1;k)=F(π2|k2),k^2right)!

这个特例可以表达为幂级数

K(k)=π2∑n=0∞[(2n)!22nn!2]2k2ndisplaystyle K(k)=frac pi 2sum _n=0^infty left[frac (2n)!2^2nn!^2right]^2k^2n!

它等价于

K(k)=π21+(12)2k2+(1⋅32⋅4)2k4+⋯+[(2n−1)!!(2n)!!]2k2n+⋯.displaystyle K(k)=frac pi 2left1+left(frac 12right)^2k^2+left(frac 1cdot 32cdot 4right)^2k^4+cdots +left[frac left(2n-1right)!!left(2nright)!!right]^2k^2n+cdots right.!

其中n!!displaystyle n!!,表示双阶乘。利用高斯的超几何函数，第一类完全椭圆积分可以表达为

K(k)=π22F1(12,12;1;k2).displaystyle K(k)=frac pi 2,_2F_1left(frac 12,frac 12;1;k^2right).,!

第一类完全椭圆积分有时称为四分周期。它可以利用算术几何平均值來快速计算。

K(k)=π2agm(1,1−k2).displaystyle K(k)=frac frac pi 2mathrm agm (1,sqrt 1-k^2).

复数值

ℜ[K(x+yi)]=π2F2×1×14×0×0[34,34,54,54,;;;1,32;12;32;−y2,x2]+π8xF2×1×14×0×0[14,14,34,34,;;;1,12;12;12;−y2,x2]displaystyle Re left[K(x+yrm i)right]=frac pi 2F_2times 1times 1^4times 0times 0beginbmatrixfrac 34,frac 34,frac 54,frac 54,;;;\1,frac 32;frac 12;frac 32;\-y^2,x^2endbmatrix+frac pi 8xF_2times 1times 1^4times 0times 0beginbmatrixfrac 14,frac 14,frac 34,frac 34,;;;\1,frac 12;frac 12;frac 12;\-y^2,x^2endbmatrix,!

ℑ[K(x+yi)]=π8yF2×1×14×0×0[34,54,34,54,;;;1,32;32;12;−y2,x2]+964πxyF2×1×14×0×0[54,74,74,54,;;;2,32;32;32;−y2,x2]displaystyle Im left[K(x+yrm i)right]=frac pi 8yF_2times 1times 1^4times 0times 0beginbmatrixfrac 34,frac 54,frac 34,frac 54,;;;\1,frac 32;frac 32;frac 12;\-y^2,x^2endbmatrix+frac 964pi xyF_2times 1times 1^4times 0times 0beginbmatrixfrac 54,frac 74,frac 74,frac 54,;;;\2,frac 32;frac 32;frac 32;\-y^2,x^2endbmatrix,!

特殊值

K(±∞)=0displaystyle K(pm infty )=0,

K(±i∞)=0displaystyle K(pm rm iinfty )=0,

K(0)=π2displaystyle K(0)=frac pi 2!

K(1)=∞displaystyle K(1)=infty !

K(22)=8πΓ2(−14)πdisplaystyle K(frac sqrt 22)=frac 8pi Gamma ^2left(-frac 14right)sqrt pi ,

K(17−122)=(4+22)πΓ2(−14)πdisplaystyle Kleft(sqrt 17-12sqrt 2right)=frac (4+2sqrt 2)pi Gamma ^2left(-frac 14right)sqrt pi ,

K(6−24)=43⋅348πΓ3(13)displaystyle Kleft(frac sqrt 6-sqrt 24right)=frac sqrt[3]4cdot sqrt[4]38pi Gamma ^3left(frac 13right),

K(6+24)=43⋅2748πΓ3(13)displaystyle Kleft(frac sqrt 6+sqrt 24right)=frac sqrt[3]4cdot sqrt[4]278pi Gamma ^3left(frac 13right),

K(−1)=2π8πΓ2(14)displaystyle K(-1)=frac sqrt 2pi 8pi Gamma ^2left(frac 14right),

K(2)=42ππΓ2(14)+42ππΓ2(14)idisplaystyle K(sqrt 2)=frac 4sqrt 2pi pi Gamma ^2left(frac 14right)+frac 4sqrt 2pi pi Gamma ^2left(frac 14right)rm i,

K(ik)=1k2+1K(k2k2+1)displaystyle K(rm ik)=frac 1sqrt k^2+1Kleft(sqrt frac k^2k^2+1right),

其中

Γ(14)≈3.62561displaystyle Gamma left(frac 14right)approx 3.62561,

Γ(13)≈2.67893displaystyle Gamma left(frac 13right)approx 2.67893,

第一类完全椭圆积分满足

E(k)K′(k)+E′(k)K(k)−K(k)K′(k)=π2displaystyle E(k)K'(k)+E'(k)K(k)-K(k)K'(k)=frac pi 2,

导数

ddkKn(k)=nKn−1(k)E(k)2k(1−k)−nKn(k)2kdisplaystyle frac rm drm dkK^n(k)=frac nK^n-1(k)E(k)2k(1-k)-frac nK^n(k)2k

漸近表示

K(k2)≈π2+π8k21−k2−π16k41−k2displaystyle K(k^2)approx frac pi 2+frac pi 8frac k^21-k^2-frac pi 16frac k^41-k^2

這個近似在k<1/2時相對誤差小於.mw-parser-output .seriffont-family:Times,serif3×10⁻⁴，若只保留前兩項則誤差在k<1/2時小於0.01

微分方程

此函數滿足以下微分方程

ddk[k(1−k2)dK(k)dk]=kK(k)displaystyle frac mathrm d mathrm d kleft[k(1-k^2)frac mathrm d K(k)mathrm d kright]=kK(k)

此微分方程之另一解為K(1−k2)displaystyle K(sqrt 1-k^2)，此解滿足以下關係。

ddkK(1−k2)=E(k)k(1−k2)−K(k)kdisplaystyle frac mathrm d mathrm d kK(sqrt 1-k^2)=frac E(k)k(1-k^2)-frac K(k)k.

第二类完全椭圆积分

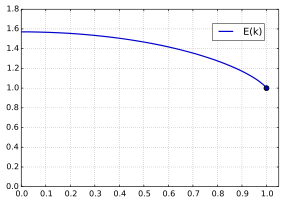
第二类完全椭圆积分E(k)displaystyle E(k)

第二类完全椭圆积分 Edisplaystyle E,可以定义为

E(k)=∫0π21−k2sin2⁡θ dθdisplaystyle E(k)=int _0^frac pi 2sqrt 1-k^2sin ^2theta rm dtheta !

或者

E(k)=∫011−k2t21−t2 dt.displaystyle E(k)=int _0^1frac sqrt 1-k^2t^2sqrt 1-t^2 rm dt.!

它是第二类不完全椭圆积分的特殊情况：

E(k)=E(1;k)=E(π2|k2),k^2)!

它可以用幂级数表达

E(k)=π2∑n=0∞[(2n)!22nn!2]2k2n1−2ndisplaystyle E(k)=frac pi 2sum _n=0^infty left[frac (2n)!2^2nn!^2right]^2frac k^2n1-2n!

也就是

E(k)=π21−(12)2k21−(1⋅32⋅4)2k43−⋯−[(2n−1)!!(2n)!!]2k2n2n−1−⋯.displaystyle E(k)=frac pi 2left1-left(frac 12right)^2frac k^21-left(frac 1cdot 32cdot 4right)^2frac k^43-cdots -left[frac left(2n-1right)!!left(2nright)!!right]^2frac k^2n2n-1-cdots right.!

用高斯超几何函数表示的话，第二类完全椭圆积分可以写作

E(k)=π22F1(−12,12;1;k2).displaystyle E(k)=frac pi 2,_2F_1left(-frac 12,frac 12;1;k^2right).,!

有如下性质

E(nπ2;k)=nE(k)displaystyle E(frac npi 2;k)=nE(k),!

n∈Zdisplaystyle nin mathbb Z ,!

复数值

E(x+yi)=π2F2×1×14×0×0[34,54,14,34,;−;−;1,32;12;32;−y2,x2]−π8xF2×1×14×0×0[14,34,−14,14,;−;−;1,12;12;12;−y2,x2]+i−π8yF2×1×14×0×0[34,54,14,34,;−;−;1,32;12;32;−y2,x2]−364πxyF2×1×14×0×0[54,74,34,54,;−;−;2,32;32;32;−y2,x2]displaystyle E(x+yrm i)=leftfrac pi 2F_2times 1times 1^4times 0times 0beginbmatrixfrac 34,frac 54,frac 14,frac 34,;-;-;\1,frac 32;frac 12;frac 32;\-y^2,x^2endbmatrix-frac pi 8xF_2times 1times 1^4times 0times 0beginbmatrixfrac 14,frac 34,-frac 14,frac 14,;-;-;\1,frac 12;frac 12;frac 12;\-y^2,x^2endbmatrixright+rm ileft-frac pi 8yF_2times 1times 1^4times 0times 0beginbmatrixfrac 34,frac 54,frac 14,frac 34,;-;-;\1,frac 32;frac 12;frac 32;\-y^2,x^2endbmatrix-frac 364pi xyF_2times 1times 1^4times 0times 0beginbmatrixfrac 54,frac 74,frac 34,frac 54,;-;-;\2,frac 32;frac 32;frac 32;\-y^2,x^2endbmatrixright,!

特殊值

E(0)=π2displaystyle E(0)=frac pi 2!

E(1)=1displaystyle E(1)=1!

E(∞)=i∞displaystyle E(infty )=rm iinfty ,

E(−∞)=∞displaystyle E(-infty )=infty ,

E(i∞)=(22−22i)∞displaystyle E(rm iinfty )=(frac sqrt 22-frac sqrt 22rm i)infty ,

E(i)=2π2πΓ2(34)+2ππ24πΓ2(34)=π2πΓ2(14)+2π8πΓ2(14)displaystyle E(rm i)=frac sqrt 2pi 2pi Gamma ^2left(frac 34right)+frac sqrt 2pi pi ^24pi Gamma ^2left(frac 34right)=frac pi sqrt 2pi Gamma ^2left(frac 14right)+frac sqrt 2pi 8pi Gamma ^2left(frac 14right),

E(−i∞)=(22+22i)∞displaystyle E(-rm iinfty )=(frac sqrt 22+frac sqrt 22rm i)infty ,

E(22)=π32Γ(14)−2+18πΓ(14)2displaystyle Eleft(tfrac sqrt 22right)=pi ^frac 32Gamma left(tfrac 14right)^-2+tfrac 18sqrt pi Gamma left(tfrac 14right)^2

E(6−24)=23⋅ 343Γ3(13)π2+43(334+274)48πΓ3(13)displaystyle Eleft(frac sqrt 6-sqrt 24right)=frac sqrt[3]2cdot sqrt[4]33Gamma ^3left(frac 13right)pi ^2+frac sqrt[3]4left(3sqrt[4]3+sqrt[4]27right)48pi Gamma ^3left(frac 13right)!

E(6+24)=23⋅ 2743Γ3(13)π2+43(274−34)16πΓ3(13)displaystyle Eleft(frac sqrt 6+sqrt 24right)=frac sqrt[3]2cdot sqrt[4]273Gamma ^3left(frac 13right)pi ^2+frac sqrt[3]4left(sqrt[4]27-sqrt[4]3right)16pi Gamma ^3left(frac 13right)!

E(2−1)=π8[Γ(18)Γ(58)+Γ(58)Γ(98)]displaystyle E(sqrt 2-1)=frac sqrt pi 8left[frac Gamma (frac 18)Gamma (frac 58)+frac Gamma (frac 58)Gamma (frac 98)right]!

E(2)=12πΓ2(34)+12πΓ2(34)idisplaystyle E(sqrt 2)=sqrt frac 12pi Gamma ^2left(frac 34right)+sqrt frac 12pi Gamma ^2left(frac 34right)rm i

其中

Γ(18)≈7.53394displaystyle Gamma left(frac 18right)approx 7.53394,

Γ(58)≈1.43452displaystyle Gamma left(frac 58right)approx 1.43452,

Γ(98)≈0.94174displaystyle Gamma left(frac 98right)approx 0.94174,

Γ(34)≈1.22541displaystyle Gamma left(frac 34right)approx 1.22541,

导数、積分及微分方程

ddkE(k)=E(k)−K(k)kdisplaystyle frac mathrm d mathrm d kE(k)=frac E(k)-K(k)k

∫E(k)dk=23[kK(k)−K(k)+kE(k)+E(k)]displaystyle int E(k)rm dk=frac 23left[kK(k)-K(k)+kE(k)+E(k)right]

(k2−1)ddk[kdE(k)dk]=kE(k)displaystyle (k^2-1)frac mathrm d mathrm d kleft[k;frac mathrm d E(k)mathrm d kright]=kE(k)

此微分方程之另解為E(1−k2)−K(1−k2)displaystyle E(sqrt 1-k^2)-K(sqrt 1-k^2)。

第三类完全椭圆积分

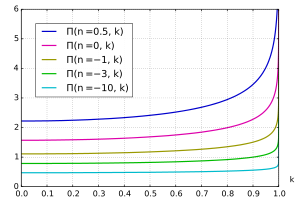
不同ndisplaystyle n值的第三类完全椭圆积分Π(n,k)displaystyle Pi (n,k)

第三类完全椭圆积分Πdisplaystyle Pi ,可以定义为

Π(n,k)=∫0π2 dθ(1−nsin2⁡θ)1−k2sin2⁡θdisplaystyle Pi (n,k)=int _0^frac pi 2frac rm dtheta (1-nsin ^2theta )sqrt 1-k^2sin ^2theta

注意有时第三类椭圆积分被定义为带相反符号的ndisplaystyle n,，也即

Π′(n,k)=∫0π2 dθ(1+nsin2⁡θ)1−k′2sin2⁡θ.displaystyle Pi '(n,k)=int _0^frac pi 2frac rm dtheta (1+nsin ^2theta )sqrt 1-k'^2sin ^2theta .

用阿佩尔函数可表示为

Π(m,n)=π2F1(12;1,12;1;m,n)displaystyle Pi (m,n)=frac pi 2F_1left(frac 12;1,frac 12;1;m,nright),

第三类完全椭圆积分和第一类椭圆积分之间的关系

Π[(1+x)(1−3x)(1−x)(1+3x),(1+x)3(1−3x)(1−x)3(1+3x)]−1+3x6xK[(1+x)3(1−3x)(1−x)3(1+3x)]=displaystyle Pi left[frac (1+x)(1-3x)(1-x)(1+3x),frac (1+x)^3(1-3x)(1-x)^3(1+3x)right]-frac 1+3x6xKleft[frac (1+x)^3(1-3x)(1-x)^3(1+3x)right]=,

{0for 0<x<1−π(x−1)(x−1)(1+3x)12xfor x<0,x>1displaystyle begincases0&mboxfor 0<x<1!,\-frac pi (x-1)sqrt (x-1)(1+3x)12x&mboxfor x<0,x>1!,\endcases

如

K(22)=π4πΓ2(14)=3−63−92Π(1−23−32,12)displaystyle Kleft(frac sqrt 22right)=frac sqrt pi 4pi Gamma ^2left(frac 14right)=frac 3-sqrt 6sqrt 3-92Pi left(frac 1-sqrt 2sqrt 3-32,frac 12right),

=3+63−92Π(1+23−32,12)−π2+3+7+3893displaystyle =frac 3+sqrt 6sqrt 3-92Pi left(frac 1+sqrt 2sqrt 3-32,frac 12right)-pi sqrt 2+sqrt 3+sqrt 7+frac 389sqrt 3,

偏导数

∂∂nΠ(n,k)=12(k2−n)(n−1)[E(k)+(k2−n)K(k)n+(n2−k2)Π(n,k)n]displaystyle frac partial partial nPi (n,k)=frac 12(k^2-n)(n-1)left[E(k)+frac (k^2-n)K(k)n+frac (n^2-k^2)Pi (n,k)nright]

∂∂kΠ(n,k)=kn−k2[E(k)k2−1+Π(n,k)]displaystyle frac partial partial kPi (n,k)=frac kn-k^2left[frac E(k)k^2-1+Pi (n,k)right]

特殊值

Π(0,0)=π2displaystyle Pi (0,0)=frac pi 2,

Π(n,0)=π21−ndisplaystyle Pi (n,0)=frac pi 2sqrt 1-n,

Π(n,1)=−∞sgn⁡n−1displaystyle Pi (n,1)=-frac infty operatorname sgn n-1,

Π(n,n)=E(n)1−ndisplaystyle Pi (n,sqrt n)=frac E(n)1-n,

Π(0,n)=K(n)displaystyle Pi (0,sqrt n)=K(n),

Π(±∞,n)=0displaystyle Pi (pm infty ,sqrt n)=0,

Π(n,±∞)=0displaystyle Pi (n,pm infty )=0,

函數關係

勒讓得闗係:

K(k)E(1−k2)+E(k)K(1−k2)−K(k)K(1−k2)=π2.displaystyle K(k)Eleft(sqrt 1-k^2right)+E(k)Kleft(sqrt 1-k^2right)-K(k)Kleft(sqrt 1-k^2right)=frac pi 2.

参看

• 椭圆曲线


• 施瓦茨-克里斯托费尔映射


• 雅可比橢圓函數


• 魏爾斯特拉斯橢圓函數


• Θ函數


• 算术-几何平均数

参考

• Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4. (See chapter 17).


• 
  Harris Hancock Lectures on the theory of Elliptic functions (New York, J. Wiley & sons, 1910)


• 
  Alfred George Greenhill The applications of elliptic functions (New York, Macmillan, 1892)


• Louis V. King On The Direct Numerical Calculation Of Elliptic Functions And Integrals (Cambridge University Press, 1924)