njtynhj

  提示：本条目的主题不是测度空间。

在数学中，度量空间是个具有距離函數的集合，該距離函數定義集合內所有元素間之距離。此一距離函數被稱為集合上的度量。

度量空间中最符合人们对于现实直观理解的為三维欧几里得空间。事实上，“度量”的概念即是欧几里得距离四个周知的性质之推广。欧几里得度量定义了两点间之距离为连接這兩點的直线段之长度。此外，亦存在其他的度量空間，如橢圓幾何與雙曲幾何，而在球體上以角度量測之距離亦為一度量。狭义相對論使用雙曲幾何的雙曲面模型，作為速度之度量空間。

度量空间还能導出开集與闭集之類的拓扑性质，这导致了对更抽象的拓扑空间之研究。

历史

莫里斯·弗雷歇在1906年于著作《Sur quelques points du calcul fonctionnel》, Rendic. Circ. Mat. Palermo 22(1906) 1–74 中引入了度量空间。

定义

度量空间是個有序對 (M,d)，这里的 M 是集合而 d 是在 M 上的度量(metric)，即為函数

d:M×M→Rdisplaystyle d:Mtimes Mrightarrow mathbb R

使得對於任何在 M 內的 x、y、z，下列條件均成立：

1. 
   d(x, y) ≥ 0 (非负性)


2. 
   d(x, y) = 0 当且仅当 x = y (不可区分者的同一性)


3. 
   d(x, y) = d(y, x) (对称性)


4. 
   d(x, z) ≤ d(x, y) + d(y, z) (三角不等式)。

條件 1 可由其他三個條件中導出^[1]。條件 1 做为度量空间的性质更恰当一些，但是很多课本都將其包含於定义之中。

函数 d 亦稱為“距离函数”或简稱“距离”。若依上下文可知道使用的度量為何，通常會省略 d，只寫出 M 為度量空間。

若不考量數學上的細節，對於任何道路系統與地形，兩個位置間之距離可被定義為連接這些位置的最短路徑之長度。度量內不應該存在單行道。三角不等式表示每個彎路都不會是最短路徑。下面的許多例子均可被視為此類一般概念的具體版本。

度量空间的例子

• 具有由絕對值給出的距離函數 d(x,y)=|y−x|displaystyle d(x,y)=vert y-xvert 之實數集合，以及更一般性地，具有歐幾里得距離之 ndisplaystyle n 維歐氏空間，這些空間均為完備度量空間。具有相關度量的有理數集合也會形成一個度量空間，但不完備。


• 具有距離函數 d(x,y)=|log⁡(y/x)|displaystyle d(x,y)=vert log(y/x)vert 的正實數集合為完備度量空間。


• 
  雙曲平面是個度量空間。


• 每個賦範向量空間都是度量空間，其度量可定義為 d(x,y)=‖y−x‖displaystyle d(x,y)=lVert y-xrVert 。若此類空間為完備的，則稱之為巴拿赫空間。例如：
  
  • 
    曼哈顿范数會形成曼哈顿距离。其中，任何两点或向量之间的距离為对应坐标间差距之和。
  
  
  • 
    极大范数會形成切比雪夫距离（或稱為棋盘距离），為国王在棋盤上从 xdisplaystyle x 移动到 ydisplaystyle y 的所需最小步数。
  
  


• 
  賦範向量空間上的英國鐵路度量（亦稱為郵局度量或法國鐵路度量）定義為 d(x,y)=‖x‖+‖y‖displaystyle d(x,y)=lVert xrVert +lVert yrVert ，其中 x 與 y 為不同的點，且 d(x,x)=0displaystyle d(x,x)=0。更一般性地，‖.‖displaystyle lVert .rVert 可用由任意集合 Sdisplaystyle S 映射至非負實數，且 0displaystyle 0 至多出現一次的函數 fdisplaystyle f 替代：則集合 S 上的度量可定義為 d(x,y)=f(x)+f(y)displaystyle d(x,y)=f(x)+f(y)，其中 xdisplaystyle x 與 ydisplaystyle y 為不同的點，且 d(x,x)=0displaystyle d(x,x)=0。此一度量的名稱係用來影射不論旅途（或信件）的終點為何，都會經過倫敦（或巴黎）的情形。


• 若 (M,d)displaystyle (M,d) 為一度量空間，且 Xdisplaystyle X 為 Mdisplaystyle M 之子集，則 (X,d)displaystyle (X,d) 亦為一度量空間，且 ddisplaystyle d 的定義域縮限於 X×Xdisplaystyle Xtimes X。


• 离散度量，其中 d(x,y)=0displaystyle d(x,y)=0，若 x=ydisplaystyle x=y，不然 d(x,y)=1displaystyle d(x,y)=1。離散度量是個简单但重要的例子，可适用于任何非空集合。特别是，離散度量证明了对于任何非空集合，总是有一个度量空间与之关联。使用此一度量，每個點都是開球，且因此每個子集都是開放的，且該空間具有離散拓撲。


• 如果 Xdisplaystyle X 是某个集合而 Mdisplaystyle M 是度量空间，则由所有有界函数 f:X→Mdisplaystyle f:Xrightarrow M（即那些像為 Mdisplaystyle M 的有界子集之函數）所組成之集合，可透過定義對於任兩個有限函數 fdisplaystyle f 與 gdisplaystyle g，d(f,g)=supx∈Xd(f(x),g(x))displaystyle d(f,g)=sup _xin Xd(f(x),g(x))（其中 supdisplaystyle sup 為上確界），轉換成度量空間^[2]。此一度量稱之為一致度量或上確界度量，且若 M 為完備的，則此一函數空間亦為完備的。若 X 亦是個拓撲空間，則由所有從 Xdisplaystyle X 至 Mdisplaystyle M 的有界連續函數所組成之集合（具有一致度量），當 Mdisplaystyle M 為完備時，該函數空間亦為完備的。


• 
  萊文斯坦距離是衡量兩個字串 udisplaystyle u 與 vdisplaystyle v 間之差異的方法，定義為字串透過刪除、插入或取代將 udisplaystyle u 轉變成 vdisplaystyle v 所需的最少步驟。該距離可被視為一個圖中最短路徑度量的特例，亦為編輯距離的一個例子。


• 如果 Mdisplaystyle M 是连通黎曼流形，则通过把在两点之间的距离定义为连接兩點的路径(连续可微曲线)之长度的下确界，將 Mdisplaystyle M 变成度量空间。


• 如果 Gdisplaystyle G 是无向连通图，则 Gdisplaystyle G 的顶点集合 Vdisplaystyle V 可通过定义 d(x,y)displaystyle d(x,y) 为连接 xdisplaystyle x 的 ydisplaystyle y 的最短路径的长度，变成度量空间。在幾何群論裡，該度量可適用於一個群的凱萊圖上，並稱之為字度量。

• 类似的，在 3D 中在多面体的表面上的度量包括平常的度量，在表面上的距离；在多面体的边上第三个度量是路径为边的度量。例如，在单位立方体相对顶点之间的距离分别是 3displaystyle sqrt 3、5displaystyle sqrt 5 和 3displaystyle 3。


• 如果 Mdisplaystyle M 是度量空间，我们把 Mdisplaystyle M 的所有紧致子集的集合 K(M)displaystyle K(M) 变成度量空间，通过定义豪斯多夫距离 d(X,Y):=infrdisplaystyle d(X,Y):=inf lbrace r。在这个度量中，两个元素是相互邻近的，如果一个集合的所有元素邻近于另一个集合某个元素。可以证明 K(M)displaystyle K(M) 是完备的如果 Mdisplaystyle M 是完备的。


• 所有紧致度量空间(的等距类)的集合形成了关于Gromov-豪斯多夫距离的度量空间。


• 给定度量空间 (X,d)displaystyle (X,d) 和递增凹函数 f:[0,∞)→[0,∞)displaystyle f:[0,infty )rightarrow [0,infty ) 使得 f(x)=0displaystyle f(x)=0 当且仅当 x=0displaystyle x=0，则 f∘ddisplaystyle fcirc d 也是 Xdisplaystyle X 上的度量。


• 给定从任何集合 Adisplaystyle A 到度量空间 (X,d)displaystyle (X,d) 的单射函数 fdisplaystyle f，d(f(x),f(y))displaystyle d(f(x),f(y)) 定义了在 Adisplaystyle A 上的度量。

• 使用T-理论，度量空间的紧跨越(tight span)也是度量空间。紧跨越在多种类型的分析中都有用处。


• 由某些域上的所有 n×mdisplaystyle ntimes m 矩阵所組成之集合，是個具有秩距离 d(X,Y)=rank(Y−X)displaystyle d(X,Y)=mathrm rank (Y-X) 的度量空间。
  


• 
  赫呂度量用於賽局理論裡。

開集、閉集、拓撲與收斂性

每個度量空間都自然地會是個拓撲空間，且因此與一般拓撲空間有關的所有定義及定理也一樣適用於所有的度量空間。

對於度量空間 Mdisplaystyle M 內的任一點 xdisplaystyle x，可定義中心為 xdisplaystyle x，半徑為 r>0displaystyle r>0（其中，rdisplaystyle r 為一實數）的開球

B(x;r)=y∈M:d(x,y)<r.displaystyle B(x;r)=yin M:d(x,y)<r.

這些開球會形成 Mdisplaystyle M 上拓撲的基，使之成為一個拓撲空間。

具體來說，Mdisplaystyle M 的子集 Udisplaystyle U 稱之為開放的，若對於每個 Udisplaystyle U 內的 xdisplaystyle x，存在一個 r>0displaystyle r>0，使得 B(x;r)displaystyle B(x;r) 包含於 Udisplaystyle U。開集的補集為閉集。點 xdisplaystyle x 的鄰域是指 Mdisplaystyle M 內包含中心為 xdisplaystyle x 的某一開球之任何子集。

拓撲空間若可由某個度量空間形成，則稱之為可度量化空間；更進一步的細節請見烏雷松度量化定理。

度量空間 Mdisplaystyle M 內之序列 (xndisplaystyle x_n) 稱之為可收斂至極限 x∈Mdisplaystyle xin M，若且唯若對於每個 ε>0displaystyle varepsilon >0，均存在一個自然數 Ndisplaystyle N，使得 d(xn,x)<εdisplaystyle d(x_n,x)<varepsilon ，對於所有 n>Ndisplaystyle n>N。在拓撲空間內也有相對應的收斂之一般定義。

度量空間 Mdisplaystyle M 內的子集 Adisplaystyle A 是封閉的，若且唯若每個在 Adisplaystyle A 內的序列若可收斂至 Mdisplaystyle M 內的一極限，則該極限在 Adisplaystyle A 內。

度量空間的類型

完備空間

度量空間 M 稱之為完備的，若每個柯西序列均收斂於 M 內，亦即：若 d(xn,xm)→0displaystyle d(x_n,x_m)to 0，其中 n 與 m 個自趨近於無限大，則存在某個 y∈Mdisplaystyle yin M，使得 d(xn,y)→0displaystyle d(x_n,y)to 0。

每個歐氏空間都是完備的，而且該空間的每個閉子集也都是完備空間。使用絕對值度量 d(x,y)=|x−y|displaystyle d(x,y)=vert x-yvert 的有理數集合則不是完備的。

每個度量空間都有個在同構意義下唯一的完備化空間。該完備化空間是個完備空間，給定之度量空間為其稠密子集。例如，實數是有理數的完備化空間。

若 X 是空間空間 M 內的完備子集，則 X 在 M 內是封閉的。而實際上，一個空間是完備的，若且唯若該空間在任何包含該空間的度量空間內都是封閉的。

每個完備度量空間都是個貝爾空間。

有界與完全有界空間

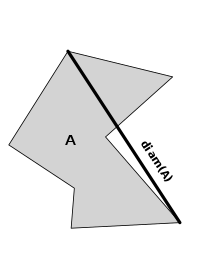
一個集合的直徑。

度量空间 M 被称为有界的，如果存在某个数 r，使得对于所有 M 中的 x 和 y 有 d(x,y) ≤ r。r 最小可能的值稱之為 M 的直徑。空间 M 稱之為预紧致的或完全有界的，如果对于所有 r > 0 存在有限多个半径為 r 的开球，其并集覆盖 M。因为这些球為有限個，所以該空間的直徑亦為有限值，从而得出(使用三角不等式)所有完全有界空间都是有界的。但逆命题不成立，因为任何无限集合均可給定其离散度量(上面第一个例子)，使得該空間是有界的，但不是完全有界的。

須注意，在討論實數空間的區間及歐氏空間的區域時，有時會將有界集合指為「有限區間」或「有限區域」。不過，有界性與「有限」之間一般並無關連；有限通常意含著有界，但反之不一定成立。

緊緻空間

度量空間 M 是緊緻的，若每個 M 內的序列均有個子序列，會收斂於 M 內的一點。這稱為序列緊緻性，且在度量空間（但不是一般拓撲空間）裡，這等價於可數緊緻與以開覆蓋定義之緊緻性等拓撲性質。

緊緻度量空間的例子包括具絕對值度量的閉區間 [0,1]、所有具有限多個點的度量空間，以及康托爾集。每個緊緻集合的閉子集亦是緊緻的。

一度量空間為緊緻的，若且唯若該空間是完備的，且為完全有界的。這即是所謂的海涅－博雷爾定理。須注意，緊緻性僅決取於拓撲，而有界性則決取於度量。

勒貝格數引理表示，對於緊緻度量空間 M 內的每個開覆蓋，均存在一個「勒貝格數」δ，使得每個 M 內直徑 < δ 的子集均會被包含於某些覆蓋內。

每個緊緻度量空間均為第二可數^[3]，且是康托爾集的連續像。（後者由帕維爾·亞歷山德羅夫與帕維爾·薩穆伊洛維奇·烏雷松所證得。）

局部緊緻與常態空間

度量空間M稱為局部緊緻的，如果每一點都有一個緊緻鄰域。歐氏空間為局部緊紗的，但無限維巴拿赫空間則不是。

度量空間M稱為常態（proper）的，如果每個閉球都是緊緻的。常態空間是完備且局部緊緻的，但局部緊緻空間未必是常態的。

連通性

度量空間 M 是連通的，若唯一同時開放或封閉的子集只有空集與 M 本身。

度量空間 M 是路徑連通的，若對於 M 內的任兩點 x、y，均存在一個連續映射 f:[0,1]→Mdisplaystyle fcolon [0,1]to M，其中 f(0)=x 且 f(1)=y。每個路徑連通空間都是連通的，但反之通常不成立。

上述性質均有相對的局部定義：局部連通空間與局部路徑連通空間。

單連通空間在某一層面上來說，可說是個沒有「洞」的空間。

可分空間

一度量空間稱之為可分空間，若該空間有可數稠密子集。典型的例子為實數或任何一個歐氏空間。對於度量空間（但不包括一般拓撲空間）可分性等價於第二可數，亦等價於林德勒夫性質。

度量空間之間的映射類型

假設 (M₁,d₁) 與 (M₂,d₂) 為兩個度量空間。

連續映射

映射 f:M₁→M₂ 是連續的，若具有下列一個（因此所有）等價性質：

一般拓撲學的連續性

對於每個在 M₂ 內的開集 U，其原像 f ^-1(U) 在 M₁ 內會是開放的。

這是在拓撲學裡連續性的一般定義。

序列連續性

若　(x_n) 是　M₁ 內一序列，且會收斂至 M₁ 內的 x，則序列 (f(x_n)) 會收斂至 M₂ 內的 f(x)。

這是由愛德華·海涅所提出的序列連續性。

ε-δ定義

對於每個在 M₁ 內的 x 及每個 ε>0，均存在 δ>0，使得對於所有 M₁ 內的 y，

d1(x,y)<δ⇒d2(f(x),f(y))<ε.displaystyle d_1(x,y)<delta Rightarrow d_2(f(x),f(y))<varepsilon .

這用到了極限的(ε, δ)定義，由奧古斯丁·路易·柯西所提出。

此外，f 是連續的，若且唯若該函數在 M₁ 的每個緊緻子集內都是連續的。

每個緊緻集合在連續函數下的像亦是緊緻的，且每個連通集合在連續函數下的像亦是連通的。

一致連續映射

映射 ƒ : M₁ → M₂ 為一致連續的，若對於每個 ε > 0，均存在 δ > 0，使得

d1(x,y)<δ⇒d2(f(x),f(y))<εfor allx,y∈M1.displaystyle d_1(x,y)<delta Rightarrow d_2(f(x),f(y))<varepsilon quad mboxfor allquad x,yin M_1.

每個一致連續映射 ƒ : M₁ → M₂ 均是連續的。若 M₁ 是緊緻的，則反向的陳述亦會成立。（海涅－康托爾定理）

一致連續映射會將 M₁ 內的柯西序列轉換成 M₂ 內的柯西序列。對於連續映射，該陳述則不一定會成立；例如，一個將開區間 (0,1) 滿射至實數線的連續映射即會將柯西序列轉換成無界的序列。

利普希茨連續映射與壓縮映射

給定一數 K > 0，映射 ƒ : M₁ → M₂ 為利普希茨連續，若

d2(f(x),f(y))≤Kd1(x,y)for allx,y∈M1.displaystyle d_2(f(x),f(y))leq Kd_1(x,y)quad mboxfor allquad x,yin M_1.

每個利普希茨連續映射均是一致連續的，但反之不一定成立。

若 K < 1，則 f 稱之為壓縮映射。令 M₂ = M₁，且 M₁ 是完備的。若 f 是個壓縮映射，則 f 會有個唯一的不動點（巴拿赫不動點定理）。若 M₁ 是緊緻的，則條件可稍微放寬一點：f 會有個唯一的不動點，若

d(f(x),f(y))<d(x,y)for allx≠y∈M1displaystyle d(f(x),f(y))<d(x,y)quad mboxfor allquad xneq yin M_1.

等距同構

映射 f:M₁→M₂ 稱之為等距同構，若

d2(f(x),f(y))=d1(x,y)for allx,y∈M1displaystyle d_2(f(x),f(y))=d_1(x,y)quad mboxfor allquad x,yin M_1

等距同構總會是單射的；緊緻或完備集合在等距同構下的像仍分別會是緊緻或完備的。不過，若等距同構不是滿射的，則閉（或開）集的像不一定是封閉（或開放）的。

擬等距同構

映射　f : M₁ → M₂　稱之為擬等距同構，若存在常數 A ≥ 1 與 B ≥ 0，使得

1Ad2(f(x),f(y))−B≤d1(x,y)≤Ad2(f(x),f(y))+B for all x,y∈M1displaystyle frac 1Ad_2(f(x),f(y))-Bleq d_1(x,y)leq Ad_2(f(x),f(y))+Btext for all x,yin M_1

且有一個常數 C ≥ 0，使得 M₂ 內的每個點與像 f(M₁) 內的某個點間之距離至多為 C。

須注意，擬等距同構不需要是連續的。擬等距同構比較度量空間的「大尺度結構」；多用於幾何群論內與字度量有關的理論。

度量空间等价性的概念

度量空間之間有著不同的等價性。依據兩個空間之間能夠存在的函數，可給出不同等價的程度與類型。

给定两个度量空间 (M₁, d₁) 和 (M₂, d₂):

• 這兩個空間稱之為同胚（拓撲同構）的，若存在兩者間的同胚（即兩個方向均為連續的雙射）。在此條件下，這兩個空間能導出相同的拓撲空間。

• 這兩個空間稱之為一致同構的，若存在兩者間的一致同構（即兩個方向均為一致連續的雙射）。

• 這兩個空間稱之為等距同構的，若存在兩者間的等距同構雙射。在此一條件下，兩個度量空間基本上是相同的。

• 這兩個空間稱之為擬等距同構的，若存在兩者間的擬等距同構。

拓扑性质

度量空間是個仿緊緻^[4]豪斯多夫空間^[5]，因此是個正規空間（且實際上是個完美正規空間）。度量空間也是個第一可數空間，因為可使用具有理數半徑的球作為該空間的基。

依據提策擴展定理，每個度量空間都能具有單位分解，且每個定義於度量空間的閉子集上之連續實數值函數均能擴展成整個空間的連續映射。每個定義於度量空間的子集上之實數值利普希茨連續映射亦能擴展成整個空間的利普希茨連續映射。

度量空間 M 上的度量拓撲是使得 M×Mdisplaystyle Mtimes M 映射至非負實數的度量 d 為連續之最粗糙拓撲。

点和集合间的距离

构造分离一个点与一个闭集的函数(作为完全正则空间的要求)的简单方式是考虑点和集合之间的距离。 如果 (M,d) 是度量空间，S 是 M 的子集而 x 是 M 的点，則可定义从 x 到 S 的距离为

d(x,S)=infd(x,s):s∈Sdisplaystyle d(x,S)=infd(x,s):sin S，其中的 infdisplaystyle inf 表示下確界。

d(x, S) = 0 若且唯若 x 包含於 S 的閉包內。此外，可將三角不等式推廣如下：

d(x,S)≤d(x,y)+d(y,S),displaystyle d(x,S)leq d(x,y)+d(y,S),

其中，可證明映射 x↦d(x,S)displaystyle xmapsto d(x,S) 是連續的。

給定兩個 M 內的子集 S 與 T，可定義豪斯多夫距離為

dH(S,T)=maxsupd(s,T):s∈S,supd(t,S):t∈Tdisplaystyle d_H(S,T)=maxsupd(s,T):sin S,supd(t,S):tin T，其中的 supdisplaystyle sup 表示上確界。

一般而言，豪斯多夫距離 d_H(S,T) 可以是無限大的。兩個集合的在豪斯多夫距離上會互相靠近，若其中一個集合的每個元素會靠近另一集合的某個元素。

豪斯多夫距離 d_H 會將由所有 M 內非空緊緻子集所組成之集合 K(M) 轉換成一個度量空間。可證明若 M 是完備的，則 K(M) 亦是完備的。（緊緻子集的收斂性亦可由庫拉托夫斯基收斂給出。）

然後，可定義任兩個度量空間之間的格羅莫夫-豪斯多夫距離為這兩個空間的等距同構嵌入版本間之最短豪斯多夫距離。使用此一距離，由所有（等距同構類型的）緊緻度量空間所組成的類本身即會形成一個度量空間。

积度量空间

如果 (M1,d1),…,(Mn,dn)displaystyle (M_1,d_1),ldots ,(M_n,d_n) 是度量空间，而 N 是在 Rⁿ 上的欧几里得范数，则 (M1×…×Mn,N(d1,…,dn))displaystyle Big (M_1times ldots times M_n,N(d_1,ldots ,d_n)Big ) 亦為度量空間，且積度量定義為

N(d1,...,dn)((x1,…,xn),(y1,…,yn))=N(d1(x1,y1),…,dn(xn,yn)),displaystyle N(d_1,...,d_n)Big ((x_1,ldots ,x_n),(y_1,ldots ,y_n)Big )=NBig (d_1(x_1,y_1),ldots ,d_n(x_n,y_n)Big ),

積度量導出之拓撲等價於積拓撲。依據有限維的範數之等價性，曼哈頓範數、p-範數、最大範數，及其他當座標內的分量增加時不會減少（符合三角不等式）之範數，所給出的度量均為拓撲同構。

同樣的，度量空间的可数積度量可以定義為如下度量：

d(x,y)=∑i=1∞12idi(xi,yi)1+di(xi,yi).displaystyle d(x,y)=sum _i=1^infty frac 12^ifrac d_i(x_i,y_i)1+d_i(x_i,y_i).

度量空間的不可數積度量不一定是可度量化的。例如， RRdisplaystyle mathbf R ^mathbf R 不是第一可數空間，因此不能度量化。

距离的连续性

值得注意的是，在一個空间 (M,d)displaystyle (M,d) 中，距离映射 d:M×M→R+displaystyle d:Mtimes Mrightarrow R^+ 在上述任何一個積度量 N(d,d)displaystyle N(d,d) 下均是一致连续的，且特别是，在 M×Mdisplaystyle Mtimes M 下的积拓扑會是连续的。

商度量空间

若 M 為度量空間，其度量為 d，且 ~ 為 M 上之等價關係，則可在商集合 M/~ 上賦加下面的（偽）度量。給定兩個等價類 [x] 與 [y]，可定義

d′([x],[y])=infd(p1,q1)+d(p2,q2)+⋯+d(pn,qn)displaystyle d'([x],[y])=infd(p_1,q_1)+d(p_2,q_2)+dotsb +d(p_n,q_n)

其中，[p1]=[x]displaystyle [p_1]=[x]、[qi]=[pi+1]displaystyle [q_i]=[p_i+1]、[qn]=[y]displaystyle [q_n]=[y]（即取從 [x] 至 [y] 經過所有等價類之路徑的最短長度）。一般來說，這僅能定義出一個偽度量，即 d'([x],[y])=0 不一定蘊涵 [x] = [y]。不過，對於良好的等價關係（如將多面體沿著面膠合），則會是個度量。此外，若 M 是個緊緻空間，則該度量在 M/~ 上導出之拓撲為商拓撲。

商度量 d 具有下列泛性質：若 f:(M,d)⟶(X,δ)displaystyle f:(M,d)longrightarrow (X,delta ) 是個度量空間之間的度量映射（英语：metric map）（即對於所有 x、y，δ(f(x),f(y))≤d(x,y)displaystyle delta (f(x),f(y))leq d(x,y)），滿足當 x∼y,displaystyle xsim y, 時，f(x)=f(y) 的條件，則函數 f¯:M/∼⟶Xdisplaystyle overline fcolon M/sim longrightarrow X 定義為 f¯([x])=f(x)displaystyle overline f([x])=f(x)，亦會是個度量映射 f¯:(M/∼,d′)⟶(X,δ)displaystyle overline fcolon (M/sim ,d')longrightarrow (X,delta )。

一個拓撲空間是序列的，若且唯若該空間是個度量空間的商空間。^[6]

度量空間的推廣

• 每個度量空間都自然會是個一致空間，而每個一致空間也都自然會是個拓撲空間。因此，一致空間與拓撲空間均可視為度量空間的推廣。

• 若考量上面給定之度量空間的第一個定義，放寬定義中的第二個條件，則可得到偽度量空間^[7]。若移除第三個或第四個條件，則可分別得到擬度量空間與半度量空間。

• 若距離函數的對應域為擴展實數線 R∪+∞，定義中的四個條件維持不變，則稱該空間為「擴展度量空間」或「∞displaystyle infty -度量空間」。若距離函數的對應域為某個（適當的）有序集（且三角不等式有對應的調整），則可得出「擴展超度量」這個概念。^[8]

• 
  趨近空間（英语：Approach space）是度量空間的推廣，以點對集合的距離取代點對點的距離。

• 
  連續性空間是度量空間與偏序集的推廣，用來統整度量空間與域的概念。

• 部分度量空間是為了對度量空間作最小化的推廣，使得每個點對自身的距離不再一定為零。^[9]

度量空間作為豐富範疇

有序集 (R,≥)displaystyle (mathbb R ,geq ) 可透過令 a≥bdisplaystyle ageq b 時恰有一態射 a→bdisplaystyle ato b，否則沒有態射，將之視為一個範疇。使用 + 作為張量積，0 作為單位元，該集合可變成一個么半範疇 R∗displaystyle R^*。每個度量空間 (M, d) 均可被視為 R∗displaystyle R^* 上的豐富範疇 M∗displaystyle M^*。其步驟如下：^[10]

• 令 Ob⁡(M∗):=Mdisplaystyle operatorname Ob (M^*):=M（M 內的元素為豐富範疇 M∗displaystyle M^* 之物件）。


• 對於每個 M 內的元素 X、Y，令 Hom⁡(X,Y):=d(X,Y)∈Ob⁡(R∗)displaystyle operatorname Hom (X,Y):=d(X,Y)in operatorname Ob (R^*)（M 的度量為豐富範疇 M∗displaystyle M^* 之態射）。


• 態射複合 Hom⁡(Y,Z)⊗Hom⁡(X,Y)→Hom⁡(X,Z)displaystyle operatorname Hom (Y,Z)otimes operatorname Hom (X,Y)to operatorname Hom (X,Z) 亦為 R∗displaystyle R^* 內的唯一態射，因為三角不等式 d(y,z)+d(x,y)≥d(x,z)displaystyle d(y,z)+d(x,y)geq d(x,z)。


• 單位態射 0→Hom⁡(X,X)displaystyle 0to operatorname Hom (X,X) 是唯一的，因為 0≥d(X,X)displaystyle 0geq d(X,X)。

参见

• 三角不等式


• 利普希茨连续


• 
  等距同构，压缩映射和度量映射
  


• 范数

註記

1. 
   ^ 依條件4，可知 d(x, y) + d(y, x) ≥ d(x,x)。再依條件3與條件2，可推得 2d(x, y) ≥ 0。因此，d(x, y) ≥ 0。
   


2. 
   ^ Searcóid, p. 107.
   


3. 
   ^ PlanetMath: a compact metric space is second countable 互联网档案馆的存檔，存档日期2009-02-05.
   


4. 
   ^ Rudin, Mary Ellen. A new proof that metric spaces are paracompact. Proceedings of the American Mathematical Society, Vol. 20, No. 2. (Feb., 1969), p. 603.
   


5. 
   ^ PlanetMath上metric spaces are Hausdorff的資料。
   


6. 
   ^ Goreham, Anthony. Sequential convergence in Topological Spaces. Honours' Dissertation, Queen's College, Oxford (April, 2001), p. 14
   


7. 
   ^ Pascal Hitzler and Anthony Seda, Mathematical Aspects of Logic Programming Semantics. Chapman and Hall/CRC, 2010.
   


8. 
   ^ Pascal Hitzler and Anthony Seda, Mathematical Aspects of Logic Programming Semantics. Chapman and Hall/CRC, 2010.
   


9. 
   ^ http://www.dcs.warwick.ac.uk/pmetric/
   


10. 
    ^ Lawvere 2002
    

參考資料

• 
  Dmitri Burago, Yu D Burago, Sergei Ivanov. A Course in Metric Geometry. American Mathematical Society. 2001. ISBN 0-8218-2129-6. 
  


• 
  Victor Bryant. Metric Spaces: Iteration and Application. Cambridge University Press. ISBN 0-521-31897-1. 
  


• 
  Mícheál Ó Searcóid. Metric Spaces. Springer Undergraduate Mathematics Series. 2006. ISBN 1-84628-369-8. 
  


• 
  Athanase Papadopoulos. Metric Spaces, Convexity and Nonpositive Curvature 2nd. European Mathematical Society. 2014. ISBN 978-3-03719-132-3. 
  


• 
  Lawvere, F. William. Metric spaces, generalized logic, and closed categories. Reprints in Theory and Applications of Categories. 2002, 1: 1–37. 
  


• 埃里克·韦斯坦因. Metric Space. MathWorld. 


• 埃里克·韦斯坦因. Product Metric. MathWorld. 

外部链接

• 
  Far and near — several examples of distance functions at cut-the-knot